I continued on the Machine Learning path by starting work on Neural Networks and Deep Learning to deepen my understanding of Neural Nets.

I started working on Neural Networks in the Programming Collective Intelligence book a few months ago as a way to train a search engine to learn to return better results for a query. The explanation of how Neural Networks were really operating, and why the algorithms were laid out the way they were, was an extremely brief page or two. I got the basic idea of a layer of inputs that fed through a network to return outputs, and then backpropagated based on training data to correct mistakes and improve over time. I didn’t understand what was going on with the Hidden Layer, the nodes between the input and output layers, or what was really happening with the weights and where the complicated formula for calculating the new weight of each node was coming from.

The new Neural Networks and Deep Learning book fills in that deeper understanding so well! The pace is perfect, and the author takes the time to pause to explain each step and each formula used in detail. He starts by explaining the Perceptron, the simplest node component of a Neural Network which has been around for a while, and how it could be used to create a similar logical path as a NAND gate, which meant that it can be used for any type of logical calculation since any type of computation can be built up from NAND gates.

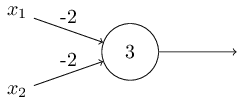
The trouble with Perceptrons is that the inputs and outputs are all binary, and so when it comes to training the network to improve results, the changes are sudden instead of gradual when the weights and biases of a node are adjusted (eg. the output suddenly flips from 1 to 0 instead of decreasing gradually). So, in order to learn, Neural Networks need to use a variation of the Perceptron called a Sigmoid Neuron, which is able to take inputs that range from 0 to 1, and outputs a number ranging from 0 to 1. Instead of a jump from 0 to 1 when the inputs * weights are greater than the bias, the sigmoid function takes the weights of all the inputs and the bias and outputs a number scaled smoothly between 0 and 1, so that incremental changes to the network’s weights and biases will make small improvements to the results that can then be optimized.

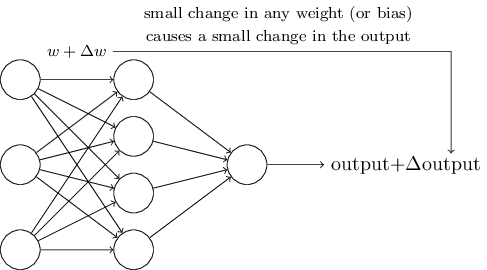
I was so excited by this section, because the sigmoid function that was unclearly derived in my earlier Neural Network explorations made perfect sense after this explanation. I got excited and actually graphed out the sigmoid function before I saw his graph a little further down because I saw that it would output larger values scaled to a max of 1 and smaller values scaled to a min of 0 for the inputs. The tone of this book is wonderful in the way that a good professor can explain conversationally a complicated topic and make everything suddenly make perfect sense.

I’m embarrassed to admit that I got a bit lost with the math in the next section. I took Multivariable Calculus, Linear Algebra, and Partial Differential Equations when I was still in high school, and since I haven’t used most of that math since then it’s a bit rusty. (Though, side note, I was pleasantly surprised to make use of MV Calc for an architecture project that involved making calculations for projecting a flat print around a spherical globe.) I tracked down my high school textbooks to review some of the concepts I couldn’t remember clearly, and learned that most of the textbooks are now available in full online! I’m looking forward to reviewing my Calculus book and Linear Algebra textbook to quickly relearn a few things, as well as browsing through some other math topics that have always interested me, such as Non-Euclidean Geometry. It’s a challenge to stay focused when there are so many amazing things to learn.

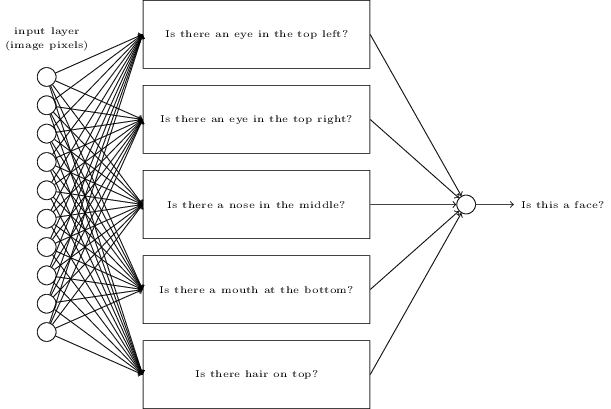
The book has a fantastic explanation of what is happening with the hidden layers of a Neural Network, and some overview of what features the hidden nodes might represent.

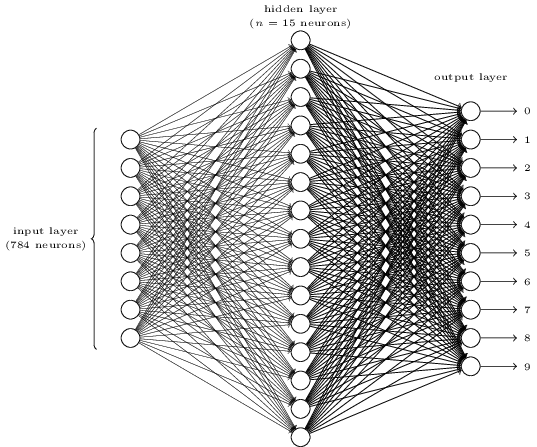
After setting up a certain number of layers and specifying the number of hidden nodes, you assign random weights and biases to each node in the network to begin. You then run the inputs through the network and check the outputs against the known correct answers. Using an optimization method similar to those used in other Machine Learning algorithms, you then attempt to find a local minimum of the error calculation for the output vs. the known answers. In order to avoid doing zillions of calculations for a large data set, you can use an optimization called Stochastic Gradient Descent to pick a random subset of inputs and optimize only on those, which with a large enough subset should approximate the values of the full dataset with a fraction of the processing time.

Super excited to continue working through this book and to learn to implement custom neural network classifiers in code!